Inhaltsverzeichnis
Simulation
Steigverhalten
Modell
Um dem Projekt soetwas wie einen wissenschaftlichen Hintergrund zu verleihen, wurden im Vorhinein ein paar Überlegungen zur Physik eines auftriebbehafteten Massesystems angestellt. Es galt zuerst, die geltenden Gesetzmäßigkeiten herzuleiten und dann eine Differentialgleichung für das Modell aufzustellen.
Die Ergebnisse dieser Arbeit sind in folgendem PDF kurz zusammengefasst: rechnung.pdf
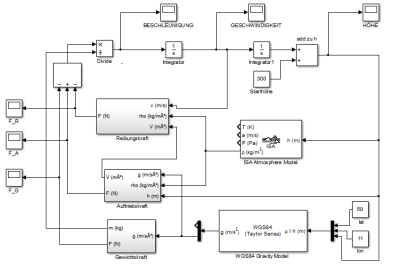
Aufgrund der hohen Flexibilität entschieden wir uns zur Lösung der DGL für einen numerischen Ansatz mit Simulink. Mit Simulink ist es unkompliziert möglich, komplexe Gleichungen im Blockschaltplan zu erstellen und numerisch lösen zu lassen. Das Blockschaltbild für die entstandene Gleichung ist im folgenden Bild zu sehen.
Ergebnisse
Diese Darstellung der DGL kann gelöst werden und führt mit den oben getroffenen Annahmen zu folgenden Ergebnissen:
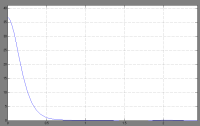
Beschleunigung (m/s^2) über Zeit (s):
Die Beschleunigung ist erwartungsgemäß direkt nach dem Loslassen groß, geht aber sofort mit Erreichen des Kräftegleichgewichts auf 0 zurück. Da Trägheit nicht eingerechnet wurde, ist kein Unterschwingen im System zu sehen.
Geschwindigkeit (m/s) über Zeit (s):
Die Geschwindigkeit erreicht bereits wenige Sekunden nach dem Start ihren Beharrungswert. Sie bleibt nahezu konstant, bis der Einfluss der dünner werdenden Luft den Auftrieb so stark reduziert, dass der Ballon irgendwann in der Luft stehen würde.
Höhe (m) über Zeit (s):
Die Höhe des Ballons verhält sich erwartungsgemäß. Zuerst ist ein Aufstieg mit relativ konstanter Geschwindigkeit zu beobachten, sobald der Auftrieb kleiner wird, wiegen sich Gewichts- und Auftriebskraft auf ein Gleichgewicht ein. Der Ballon bleibt rechnerisch in etwa 19km Höhe „hängen“.
Schlussfolgerungen
Die folgende Tabelle gibt Aufschluss über möglicherweise zu erwartende Höhen nach verschiedenen Missionsdauern:
| Flugzeit | Höhe |
|---|---|
| 15min | 7km |
| 20min | 9km |
| 25min | 11,5km |
| 30min | 12km |
Auswertung
Im echten Flug wurde eine geringere Steiggeschwindigkeit von ~300m/min erreicht. Sicherlich ist diese Zahl aber sehr v.a. von der Gasfüllmenge des Ballons abhängig!